Optimal Designs for Multi-Arm Phase II/III Drug Development Programs
Further reading: Preussler, S., Kirchner, M., Götte, H., & Kieser, M. (2021). Optimal designs for multi-arm phase II/III drug development programs. Statistics in Biopharmaceutical Research, 13(1), 71-81.
Summary
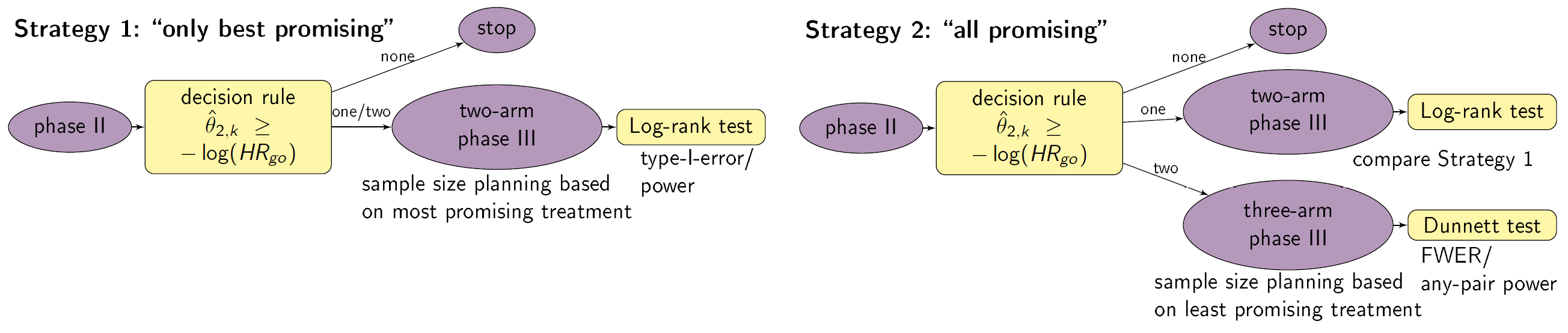
This App is a tool for phase II/III drug development planning aiming to optimize the sample size allocation and go/no-go decision rule with respect to the maximal expected utility. The approach is based on a utility function taking into account, e.g., fixed and variable costs of the program (c02, c03, c2 , c3), expected benefits after successful market launch (b1, b2, b3), assumed true hazard rates (HR1, HR2), and control arm event rates in phase II and III (ec). The considered drug development program consists of one three-arm phase II trial possibly followed (in case of a go-decision after phase II) by a phase III trial. In particular, two decision rule strategies are compared: in Strategy 1 only the best promising treatment of phase II goes to phase III, leading to a two-arm phase III trial. In Strategy 2 multiple treatments (if sufficiently promising) can go to phase III, resulting in a two- or three-arm phase III trial. Furthermore, a constraint on the total expected sample size in the trial can be specified (N).
Setting
We consider a drug development program with one exploratory phase II and one confirmatory phase III trial, which are performed independently with the same time-to-event primary endpoint and the same population. The phase II trial is a three-arm randomized trial, with 1:1:1 sample size allocation, followed by a decision rule, whether or not a phase III trial is conducted. The phase III trial can have two or three arms. Program success is the joint event of going to phase III and declaring one treatment significantly superior to the control. HRk is the true hazard ratio, i.e., the ratio between the hazard function for the experimental treatment k=1, 2 and the control group. We require that only promising treatments lead to a phase III trial: if the estimate of the HR of a treatment in phase II undershoots a predefined threshold value HRgo, the treatment is declared to be promising. In case of a go decision, the calculation of the sample size for phase III is based on the promising treatment effect estimates of phase II: for a 1:1 two-arm phase III trial the calculation of the sample size is based on the maximum of the treatment effect estimates of phase II and orientated on the Schoenfeld (1981) formula, for a three-arm phase III trial the minimum of the treatment effect estimates, the formula of Horn and Vollandt (1998) and 1:1:1 allocation ratio is used. In a two-arm phase III trail the log-rank test is performed, which controls the type-I error by α with 1- β power. In a three-arm phase III trial the Dunnett test (Dunnett, 1995) is conducted controlling the family wise error rate by α in the strong sense (Magirr et al. 2012) with 1-β any-pair power. In case the trial is successful, it is assumed that the amount of benefit depends on the value of the observed treatment effect in phase III: orientated on a report of the IQWiG (2016), three effect size categories (small, medium, large) and associated benefit categories (b1, b2,b3) are defined. Optimal designs are determined by maximizing the expected utility over n2 and HRgo.
Instructions
- Choose whether you want to investigate the design parameters of Strategy 1 only, Strategy 2 only or both.
- Select the range of n2 and HRgo over which the optimization is performed.
- Specify all other drug development program parameters.
- Choose if the table of the results should be refreshed (do not show previous results) or not (also shows previous results).
- Choose if a plot of the optimization region (of the “better” Strategy) should be plotted.
- Click on “Go” and wait until results are presented in the table below (it may take some minutes).
Values presented in table
- Strategy
- maximal expected utility (u)
- drug development planning characteristics: assumed true hazard rates (HR1, HR2), control arm event rate (ec)
- optimal threshold value for the decision rule to go to phase III (HRgo)
- optimal total sample size for phase II (n2)
- total expected sample size for phase III (n3)
- total expected sample size in the program (n)
- maximal total expected sample size in the program (N)
- probability to go to phase III (pgo)
- probability of a successful program (sProg)
- probability of a successful program with two arms in Phase III (sP2)
- probability of a successful program with three arms in Phase III (sP3)
- costs for phase II (K2)
- costs for phase III (K3)
and further input parameters. It should be noted, that “maximal” and “optimal” is with respect to the specified range of n2 and HRgo.
References
Dunnett, C. W. (1955). A multiple comparison procedure for comparing several treatments with a control. Journal of the American Statistical Association 50(272), 1096-1121.
Horn, M., and Vollandt, R. (1998). Sample sizes for comparisons of k treatments with a control based on different definitions of the power. Biometrical Journal: Journal of Mathematical Methods in Biosciences 40(5), 589-612.
IQWiG (2016). Allgemeine Methoden. Version 5.0, 10.07.2016, Technical Report. Available at https://www.iqwig.de/de/methoden/methodenpapier.3020.html, assessed last 15.05.19.
Magirr, D., Jaki, T., and Whitehead, J. (2012). A generalized Dunnett test for multi-arm multi-stage clinical studies with treatment selection. Biometrika 99(2), 494-501.
Schoenfeld, D. (1981). The asymptotic properties of nonparametric tests for comparing survival distributions. Biometrika 68(1), 316-319.
Further Software
The software drugdevelopR (available via: https://web.imbi.uni-heidelberg.de/drugdevelopR/) includes further Apps and an R package for optimal phase II/III drug development planning. The Code, detailed user manuals and application examples can be found on Github (https://github.com/Sterniii3/drugdevelopR).
Note
If the server is busy, you may need to double click the “Go”-button in order to see the updated plot.
Maintainer
Stella Erdmann, Institute of Medical Biometry, University of Heidelberg, email: erdmann@imbi.uni-heidelberg.de.
Version 1.1