Optimal Designs for Phase II/III Drug Development Programs including methods for discounting of phase II results

Further reading: Stella Preussler, Marietta Kirchner, Heiko Goette, Meinhard Kieser. Optimal designs for phase II/III drug development programs including methods for discounting of phase II results. BMC medical research methodology, 20(1), 253. https://doi.org/10.1186/s12874-020-01093-w.

Summary

This shiny App is a tool for phase II/III drug development planning aiming to optimize the sample size allocation and go/no-go decision rule with respect to the maximal expected utility. The approach is based on a utility function taking into account, e.g., fixed and variable costs of the program (c₀₂, c₀₃, c₂ , c₃), expected benefits after successful market launch (b₁, b₂, b₃), assumed true hazard rate (HR), and event rates in phase II and III (ξ_i, i=2,3). The considered drug development program consists of one phase II trial possibly followed (in case of a go-decision after phase II) by a phase III trial. A treatment effect estimate from phase II that lead to go decision generally overestimates the true treatment effect, resulting in an underpowered phase III trial. Therefore, bias adjustment methods are applied to the treatment effect estimate of phase II used for the calculation of the number of events for phase III. In particular, two (1. multiplicative by Wang et al. (2006) and 2. additive by Kirby et al. (2012)) bias adjustment methods are adapted so that optimization over their parameters can be done: 1. Multiplicative adjustment is done by multiplying the treatment effect estimate of phase II with a retention factor λ. 2. Additive adjustment is done by using the lower bound of the 1-α_CI confidence interval of the treatment effect estimate.

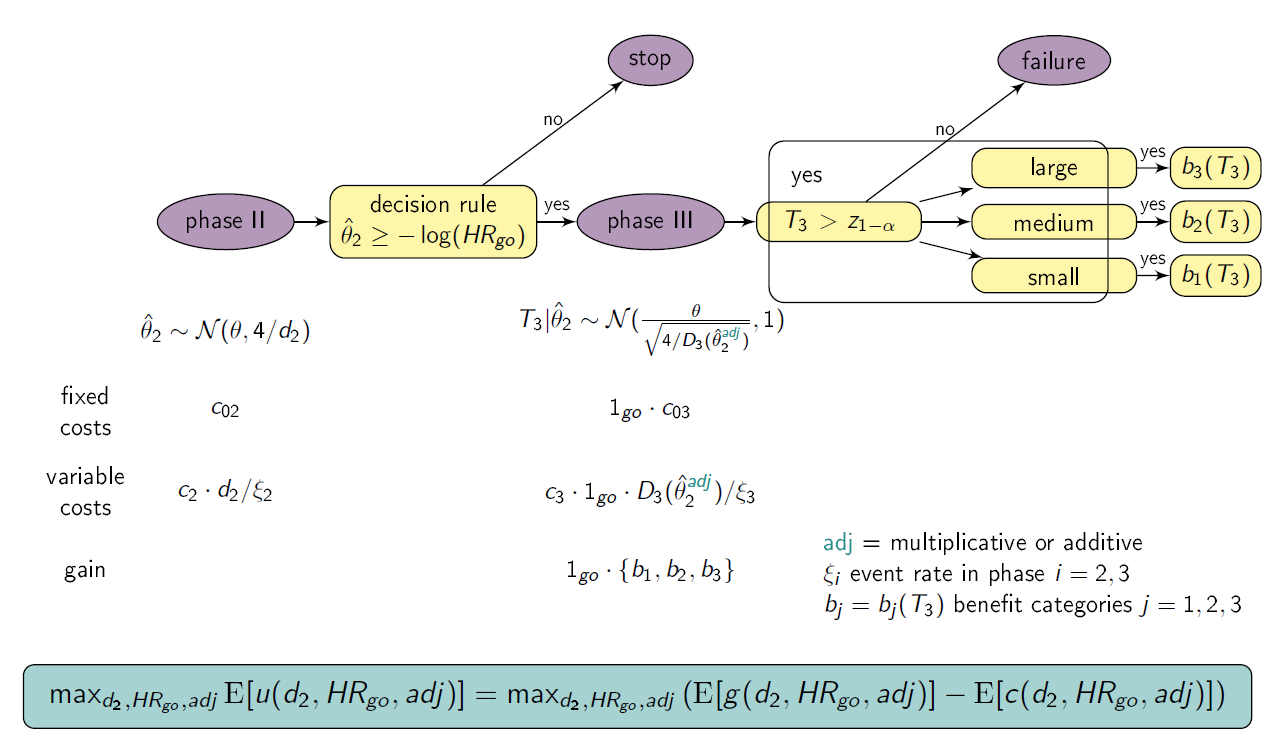
Setting

We consider a drug development program with one exploratory phase II and one confirmatory phase III trial, which are performed independently with the same time-to-event primary endpoint and the same population. The phase II trial is a two-arm randomized trial followed by a decision rule, whether or not a phase III trial (RCT) is conducted. Program success is the joint event of going to phase III and declaring the treatment significant superior to the control. The treatment effect is measured by θ=-log(HR), where HR is the true hazard ratio, i.e., the ratio between the hazard function for the experimental treatment and the control group. We require that only promising treatments lead to a phase III trial: if the treatment effect estimate of phase II θ̂₂ overshoots a predefined threshold value -log(HR_go), the treatment is declared to be promising. In case of a go decision, the calculation of the number of events for phase III is based on the promising treatment effect estimate of phase II by the Schoenfeld (1981) formula and the log-rank test is performed, which controls the type-I error by α and aims at 1- β power. As treatment effect estimates after decision rules generally overestimate the true treatment effect, the multiplicatively (θ̂₂⋅λ) and the additively adjusted treatment effect estimator (θ̂₂ - z_1-αCI⋅ √ 4/d₂, z_y is the y quantile of the standard normal distribution) is used for the calculation of the number of events for phase III, respectively. To compute the variable per-patient costs, the sample size is calculated by dividing the (expected) number of events by the event rate, i.e. n_i = d_i/ξ_i, i=2,3. In case of program success, we assume that the amount of benefit depends on the value of the observed treatment effect in phase III. Orientated on a report of the German Institute for Quality and Efficiency in Health products, three effect size categories (small, medium, large) and associated benefit categories (b₁, b₂, b₃) are defined by threshold values (1, 0.95, 0.85) which have to be undershoot by the upper boundary of the two sided (1-α)-confidence interval of the HR in phase III (IQWiG, 2016). The optimization is simultaneous done over HR_go, d₂ and λ or α_CI, respectively.

Instructions

1. Select the range of d₂, HR_go and λ and/or α_CI over which the optimization is performed.
2. Specify all other drug development program parameters.
3. Choose if the table of the results should be refreshed (do not show previous results) or not (also shows previous results).
4. Choose if a plot of the optimization region should be plotted.
5. Click on “Go” and wait until results are presented in the table below.

Values presented in table

• Method
• expected utility (u)
• assumed true hazard rate (HR)
• adjustment parameter (λ or α_CI)
• threshold value for the decision rule to go to phase III (HR_go)
• total number of events for phase II (d₂)
• total expected number of events for phase III (d₃)
• total expected number of events in the program (d)
• total sample size for phase II (n₂)
• total expected sample size for phase III (n₃)
• total expected sample size in the program (n)
• probability to go to phase III (p_go)
• probability of a successful program (sProg)
• probability of a successful program with small treatment effect (sProg1)
• probability of a successful program with medium treatment effect (sProg2)
• probability of a successful program with large treatment effect (sProg3)
• costs for phase II (K2)
• costs for phase III (K3)

and further input parameters.

References

IQWiG (2016). Allgemeine Methoden. Version 5.0, 10.07.2016, Technical Report. Available at https://www.iqwig.de/de/methoden/methodenpapier.3020.html, assessed last 15.05.19.

Kirby, S., Burke, J., Chuang-Stein, C., & Sin, C. (2012) Discounting phase 2 results when planning phase 3 clinical trials. Pharmaceutical Statistics 11(5), 373-385.

Schoenfeld, D. (1981). The asymptotic properties of nonparametric tests for comparing survival distributions. Biometrika, 68(1), 316-319.

Wang, S. J., Hung, H. M., & O’Neill, R. T. (2006). Adapting the sample size planning of a phase III trial based on phase II data. Pharmaceutical Statistics 5(2), 85-97.

Additional Features

The true underlying treatment effect θ can also be modelled by a prior distribution (https://web.imbi.uni-heidelberg.de/prior/). Optimal planning can then be done with the function optimal_bias() of the R package drugdevelopR available at: https://github.com/Sterniii3/drugdevelopR.

Note

If the server is busy, you may need to double click the “Go”-button in order to see the updated plot.

Maintainer

Stella Erdmann, Institute of Medical Biometry, University of Heidelberg, email: erdmann@imbi.uni-heidelberg.de.

Version 1.1